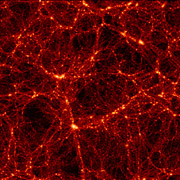
Les fractals ont été inventés par le mathématicien Benoit Mandelbrot pour décrire la géométrie de la nature, dont les formes complexes et irrégulières échappent à la géométrie classique.

Une propriété des fractals comme de la nature est l'auto-similarité, c'est à dire la répétition de formes similaires à différentes échelles d'observation. Ainsi, une partie d'un nuage ressemble au nuage tout entier, et un rocher rappelle les formes de la montagne. Une forme typiquement fractale est celle du chou-fleur, ou du brocoli, dont les parties sont exactement à l'image du tout.

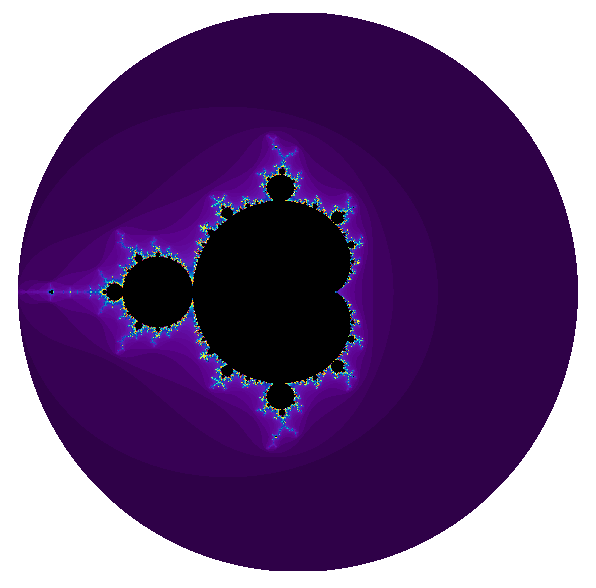
Le fractal de Mandelbrot est la visualisation d'un objet mathématique. Il s'agit en réalité d'une matrice de nombres, où la valeur de chaque nombre est représentée par une couleur.
Chaque point de l'image est un nombre calculé par l'ordinateur selon une équation très simple:
    Z_n+1 = Z_n² + C

Le plus étonnant est que, comme la nature, cette équation produit des formes complexes d'une grande beauté...